Abschnittsübersicht

    • Beispiel:
      Bestimme die Nullstellen folgender Funktion f(x) = x^2 + 32 x + 135
      Rechenweg:
      1. Null setzen der Funktionsgleichung
      x^2 + 32 x + 135 = 0

      2. pq-Formel anwenden
      x_{1/2} = - \frac{32}{2} \pm \sqrt{  \left( \frac{32}{2} \right)^2 - 135}

      bitte bei solchen Zahlen, die man im Kopf durch 2 teilen kann gleich die gekürzte Version aufschreiben

      x_{1/2} = - 16 \pm \sqrt{16^2 - 135} Tipp: Da p unterhalb der Wurzel quadriert wird, muss man sich bei der 16 keine Gedanken um das Vorzeichen machen und kann gleich 16² statt (-16)² schreiben.

      3. Ergebnisse für x
        x_{1}= -27
        x_{2}= -5

    • Wie kann man die normale Gleichung in die Schreibweise mit Linearfaktoren umwamdeln?
      Man muss die Nullstellen z.B. mit Hilfe der pq-Formel bestimmen .... schon kann man die quadratische Gleichung auch mit Linearfaktoren schreiben. Achtung: Vorzeichen beachten!!!

      Beispiel:
      f(x)=x²+2x-8


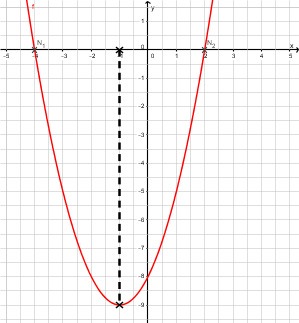
      Nullstellen bestimmen mit Hilfe von f(x)=0 . Man spricht auch von: "Null setzen"

      0=x^2+2x-8 0=x²+px+q
      p=2
      q=-8
      		 p ist die Zahl VOR!!! der Variablen x; Vorzeichen beachten!
      q ist die Zahl OHNE!!! die Variable x; Vorzeichen beachten!

      Eselsbrücke zur pq-Formel
      1. Vorzeichen ändern und halbieren (hinschreiben)...
      2. ... plus oder Minus Wurzel aus (hinschreiben) ...
      3. ... die hingeschriebene Zahl quadrieren (hinschreiben) ...
      4. ... minus q
      x_{1/2} = - 1 \pm \sqrt{ 1 - (-8) }


      Das schreibt man aber wie folgt, den -(-8) ist ja in +8:

      x_{1/2} = - 1 \pm \sqrt{ 1 +8) }

      umformen:
      x_{1/2} = - 1 \pm \sqrt{ 9 }
      x_{1/2} = - 1 \pm 3

      Somit ergeben sich die Nullstellen:
      x = -4 Nullstellen 1
      x = 2 Nullstelle 2

      Schnittpunkte mit der x-Achse sind dann so anzugeben:
      N1(-4/0)
      N2(2/0)      		 x_{1/2} = - \frac{p}{2} \pm \sqrt{ p - q }